FlowSOM: 基于自组织映射分析流式细胞数据

背景

FlowSOM(Van Gassen et al., 2015)^[1] 是一种可用于分析流式细胞术和高维数据的算法。

流式细胞仪是一种能每秒检测和测量数千个细胞或颗粒的特征的技术。 高维的流式细胞数据能够用于检测蛋白质标记物的表达，从而得以前所未有地详细表征细胞群体。简单地说，分析这种高维数据，第一步是一个聚类问题，而FlowSOM则是对应的一种方法。

据 Weber和Robinson(2016)^[2]所言，FlowSOM “能够在极短的时间内运算完毕，这使得它非常适合在普通计算机上对大型高维数据集进行交互式、探索性分析。”

算法详解

FlowSOM 利用自组织映射（SOM）来分析流式细胞数据。利用两级聚类和星形图表，FlowSOM有助于清晰而全面地理解所有细胞里被标记出的所有特征，并能够检测出容易被其他算法忽视的子集。

FlowSOM由4步组成：

• 读取数据
• 建立自组织映射
• 建立最小生成树
• 计算元聚类

读取数据

这实际上是预处理的步骤。对于同一个实验中多个fcs文件，建议将多个fcs文件合并同时训练。这样，模型能建立在完整的数据之上。

预处理方法有很多，我们将以缩放为例。一旦读取了所有文件并将它们合并到在一起，可以通过以下方式进行缩放：

$$c_{ij} = \frac{c_{ij} - mean(c_{1j},.... c_{nj})}{std(c_{1j},.... c_{nj})}$$

这使得每一列的平均值为0，标准差为1，并确保每个特征在进一步处理中具有相同的重要性。（如果专家知识指出一个标记应该比另一个标记具有更高的重要性，则可以设置特定的缩放参数。）

自组织映射

自组织映射（SOM）是一种使用在聚类问题上的人工神经网络（ANN）(Kohonen, 1990)^[3]. 它能够将高维数据项之间的复杂，非线性统计关系转换为低维上的简单几何关系。

它使用无监督学习来生成训练样本的低维（通常为二维）离散化的表示，称为映射，因此它也是进行维数减少的一种方法。

自组织映射

下图说明了如何训练自组织映射。紫色区域代表了训练数据的真实分布。小白网格是从该分布中得出的当前训练数据。起初，自组织映射的节点随机地分布在数据空间中。选择最接近训练基准的节点（黄色），将其移向真实基准，网格中的它相邻基准也随之移动。经过多次迭代后，网格趋向于近似数据分布（右）。

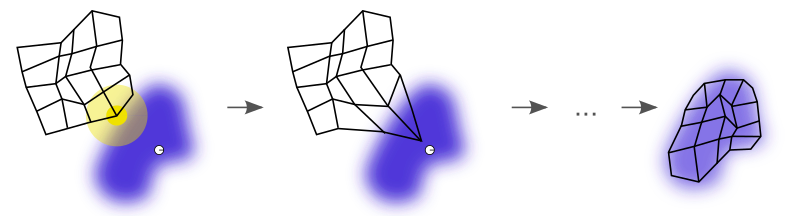自组织映射的训练

训练自组织映射分为以下几个步骤：

1. 初始化每个节点的权重。权重设置为较小的正太分布随机值。
2. 从训练集中随机选择一个向量。
3. 检查每个节点，以计算哪个节点的权重最接近被选中的向量，由此获得最佳匹配单位（BMU）。我们通过遍历所有节点并计算每个节点的权重与当前输入向量之间的欧式距离来计算BMU。具有最接近输入向量的权重向量的节点被标记为BMU。
4. 计算BMU附近的半径。在半径内找到的节点被视为在BMU近邻。
5. 调整步骤4中找到的节点的权重，使其更像输入向量。靠近BMU的节点的权重被调整得更多。
6. 重复步骤2进行N次迭代。

最小生成树

生成的自组织映射的聚类将由最小生成树（MST）可视化。 最小生成树（Whitney，1972） ^{[4] </ sup>以使分支的权重之和尽量小的方式连接图的节点。由此，基于数据的多维拓扑，节点将被连接到它们最相似的节点。简而言之，它是一个连接起来的无向图的子集，该图将所有顶点连接在一起，没有任何循环，并且总的边权重最小。}

元聚类

自组织映射其实直接得出聚类结果，只要将节点数设置为预期的聚类类型数。但是，为了更好地可视化，不妨包含比预期数量的类别更多的点。这样，介于几种类型之间的细胞也可以被标记出来，因此可以注意到细胞类型中的较小变化。

在自组织映射上进行的元聚类技术是分层共识元聚类，将SOM的权重分为不同的组。

FlowSOM的Python实现

Python代码点击这里。

参考

[1] Van Gassen, S., Callebaut, B., Van Helden, M.J., Lambrecht, B.N., Demeester, P., Dhaene, T. and Saeys, Y., 2015. FlowSOM: Using self‐organizing maps for visualization and interpretation of cytometry data. Cytometry Part A, 87(7), pp.636-645.

[2] Weber, L.M. and Robinson, M.D., 2016. Comparison of clustering methods for high‐dimensional single‐cell flow and mass cytometry data. Cytometry Part A, 89(12), pp.1084-1096.

[3] Kohonen, T., 1990. The self-organizing map. Proceedings of the IEEE, 78(9), pp.1464-1480.

[4] Whitney, V.K.M., 1972. Algorithm 422: minimal spanning tree [H]. Communications of the ACM, 15(4), pp.273-274.